Quadratic Function: Completing The Square | Prove

By
    In general, a quadratic function will have the form of f(x) = ax² + bx + c,  where a, b and c are constants and a ≠ 0.  Do remember that in order to perform the method of completing the square, the coefficient of the x² term in the quadratic expression MUST be equal to 1.

    In this case, we are going to prove 

where k is also a non-zero arbitrary constant.

    To prove and thoroughly understand how the method of completing the square works on a quadratic function, we can actually visualize it by using paper-folding technic. In order to do so, the materials that are required include an A4 sized paper, a pen, a cellophane tape and a pair of scissors or a paper cutting blade. 

    The procedures needed are as shown as follow. All the figures shown in the procedures are the top view of the A4 sized paper.

    1. Fold the A4 sized paper as shown in the figure below according to the sequence indicated.

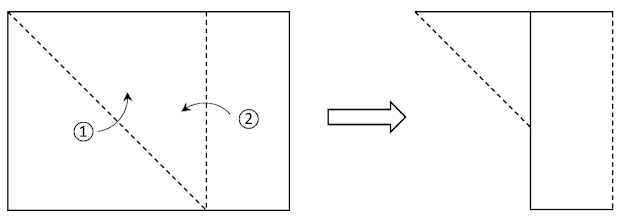
   2. Unfold the A4 sized paper and label the length of each side of the paper as shown below. Now, you shall notice that your paper is composed of two parts (i.e. a square and a rectangle).

    3. Now, fold the A4 sized paper again as shown below.

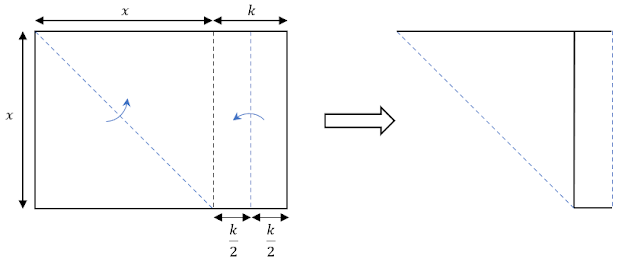
    4. Use cellophane tape to join the paper together. Then, cut the paper according to the red dotted line as shown.

    5. Unfold the paper again. Now, you shall notice that the shape of the paper had changed into some sort of a square but not exactly. 

    Now, note that the area of the paper can be expressed in another way.



    The area of the A4 sized paper does not change throughout the process.
    
    ⇒

    ⇒
(Proven)

    I hereby attached a video explanation for this section. Kindly watch it if are still uncertain about the concept behind the method of completing the square for a quadratic expression. 

    I hope you enjoyed reading the post and watching the videos as well. Lastly, please do not forget to LIKE, SHARE and SUBSCRIBE to my blog and my YouTube channel as well. Thank you and have a nice day!


Comments

Post a Comment

Popular posts from this blog

Quadratic Function: Completing The Square | Derivation

By
    In the previous post , we have proven the equation that is responsible for the method of completing the square in a quadratic function. The equation that we have proven previously is  ----------------------------------------------- (1)                         where k is a non-zero arbitrary constant.     Now, what will happen to equation (1) if the constant, k has a positive value? What if the constant, k has a negative value? Let us try to find it out.     (A) Positive Value of the Constant, k           (B) Negative Value of the Constant, k     Hence, we have derived the two equations which is normally used for the method of completing the square in an quadratic function.   Lastly, I hope that you enjoyed reading the post and learning from it. Please do not forget to  LIKE ,  SHARE  and  SUBSCRIBE  to my  blog  and my  YouTube channel  as well. Thank you and have a nice day!
Read more

Quadratic Function: Completing The Square | Verification

By
    In the  previous post , we have derived  two equations which is normally used for the method of completing the square in an quadratic function. The above-mentioned equations are shown below, where the constant, m has a positive value.     Today, we will verify the two equations above to ensure that the two equations are valid. To verify these equations, what we have to do is to expand and simplify the right hand side (RHS) of the equations and compare it with the left hand side (LHS) of the equations. As long as RHS = LHS, the equation will be true.     Equation (1)     Equation (2)        As we can see, the two equations which is normally used for the method of completing the square in an quadratic function have been verified.   I hope that you enjoyed reading the post and learning from it. Please do not forget to  LIKE ,  SHARE  and  SUBSCRIBE  to my  blog  and my  YouTube channel  as well. Thank you and see you in the next blog post!
Read more