Quadratic Function: Quadratic Formula | Axis of Symmetry

By
The Quadratic Formula:

    Previously, we have proven the Quadratic Formula which is used to find the roots of a particular quadratic function. As we know, the graphical representation of a quadratic function is having a symmetrical shape. Having said that, there will be a line(axis) of symmetry in the graph of any quadratic function. 

    Base on the Quadratic Formula, every quadratic function will have two roots in general. These roots are 

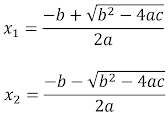
    Since the graph of any quadratic function is having a symmetrical shape, hence the axis of symmetry must be equidistance from both its roots. In another words, the axis of symmetry is located at the midpoint of horizontal line connecting both the roots. Hence, the equation for the axis of symmetry can be determined by finding the midpoint between x₁ and x₂.


    By doing so, we have successfully derived the equation for the axis of symmetry for a quadratic function based on the Quadratic Formula. What other information that we can obtain from the Quadratic Formula? We will discuss it further in the next post. Stay tuned! Before that, don't forget to LIKE, SHARE and SUBSCRIBE to my blog and also my YouTube channel. See you!

Comments

Post a Comment

Popular posts from this blog

Quadratic Function: Completing The Square | Prove

By
     In general, a quadratic function will have the form of  f(x) = ax ² + bx + c ,    where a, b and c are constants and a  ≠ 0.    Do remember that in order to perform the method of completing the square, the coefficient of the  x ²  term in the quadratic expression  MUST  be equal to 1.      In this case, we are going to prove  where k is also a non-zero arbitrary constant.     To prove and thoroughly understand how the method of completing the square works on a quadratic function, we can actually visualize it by using paper-folding technic. In order to do so, the materials that are required include an A4 sized paper, a pen, a cellophane tape and a pair of scissors or a paper cutting blade.      The procedures needed are as shown as follow. All the figures shown in the procedures are the top view of the A4 sized paper.     1.  Fold the A4 sized paper as shown in the figure below according to the sequence indicated.    2. Unfold the A4 sized paper and l abel the length of each side o
Read more

Quadratic Function: Quadratic Formula | Prove

By
     As we have discussed earlier, a general quadratic function  will have the form of  f(x) = ax ² + bx + c ,    where a, b and c are constants and a  ≠  0. Now, I would like to the quadratic formula to you. What exactly is a quadratic formula? A quadratic formula is used to solve a given quadratic function. When we talk about solving a quadratic function, it simply means finding the roots of the quadratic function. Some of you might be curious what is a root? The root that the plant has in their system? No!! The roots of a quadratic function refer the the positions (values of x) on the x-axis at which the quadratic function intersect with the x-axis in a Cartesian Plane. The quadratic formula is given as      Today, we will going to prove the quadratic formula shown above by using the method of Completing The Square . We will start from the general quadratic function. (Proven)           Hence, we have proven the Quadratic Formula which is used to find the roots of a particular quadra
Read more